When they are asked to evaluate diagnostic tests, panels can apply criteria that are similar to those used for other health interventions that come before the Medicare Coverage Advisory Committee. The panels will need to determine whether the evidence is adequate to conclude that the diagnostic test improves outcomes and, if the evidence is adequate, to classify the magnitude of the health benefit, when a test is used for a specific purpose.
When more than one application of the test is under consideration, the panels will need to evaluate each application. Although this document refers to diagnostic tests, it is important to recognize that tests have four principal uses in clinical settings, and that the comments in this document refer to all four uses.
Screening: screening refers to the use of a test to detect either asymptomatic disease or a predisposition to disease (i.e., a risk factor such as elevated blood pressure or high blood cholesterol). Typically, the pre-test probability of disease (i.e., the prevalence or probability of disease in the population to be screened) is very low in such individuals. The purpose of screening is either to take action to prevent disease by modifying a risk factor, or to detect and treat disease early. In both cases, screening is presumed to be advantageous because early treatment of disease, or modification of a risk factor, improves health outcomes.
Diagnosis: a test is used to make a diagnosis when symptoms, abnormalities on physical examination, or other evidence suggests but does not prove that a disease is present. Making a correct diagnosis improves health outcomes by leading to better clinical decisions about further testing and/or treatment.
Staging: a test is used to stage a disease when the diagnosis is known but the extent of disease is not known. Staging is particularly important when stage of disease, as well as the diagnosis itself, influences management. For example, an early stage cancer might be treated surgically, while the same cancer at a more advanced stage might be treated with chemotherapy alone.
Monitoring: in a patient known to have a health condition, a test is used to monitor the disease course or the effect of therapy. A monitoring test helps to evaluate the success of treatment and the need for additional testing or treatment.
Although an effective diagnostic test reduces the morbidity and mortality of disease by guiding clinical decisions, direct proof of effectiveness is usually unavailable. Few studies have directly measured the effects of a diagnostic or screening test on health outcomes (studies of occult blood testing for colon cancer represent one such exception). Typical studies that evaluate the effectiveness of diagnostic, screening, or monitoring tests focus either on technical characteristics (e.g., does a new radiographic test produce higher resolution images) or effects on accuracy (does it distinguish between patients with and without a disease better than another test).
An improvement in the technical performance of a test can lead to improved diagnostic accuracy. For example, a higher resolution imaging study is more likely to distinguish between normal and abnormal anatomic structures, since it is able to delineate both types of structures more clearly. It may seem self-evident that improved technical characteristics would routinely lead to greater test accuracy and clinical utility, but that is not always the case. Often the factor that limits the ability of a test to distinguish between diseased and non-diseased, or between a person at high risk for disease and a person at average risk, is not the technical performance of the test. Sometimes the indicator that we are trying to measure (e.g., the risk factor) is only imperfectly correlated with the health condition, and improved measurement of the indicator will not lead to greater accuracy. Occasionally technical performance can improve in one respect but worsen in another; for example, MRI scans have higher resolution than most CT scans. Thus MRI scans were initially believed to be superior to CT scans for most indications. However, because CT scans are better able to distinguish certain tissue types, they proved to be better at detecting some abnormalities than the higher-resolution MRI scans. Thus improvements in aspects of technical performance are not sufficient to establish improved diagnostic accuracy.
When good quality studies directly measure how the use of a diagnostic test affects health outcomes, the panel can easily determine that the evidence is adequate and draw conclusions about the magnitude of the health benefits. But when the best studies only measure the accuracy of the test itself, the panels will have to determine whether the evidence is adequate to conclude that the test improves the accuracy of diagnosis or staging of disease and that the improvement in accuracy leads to better health outcomes.
We suggest that panels evaluating diagnostic test answer the following question:
Is the evidence adequate to conclude that the use of the diagnostic test leads to a clinically significant improvement in health outcomes?
If direct evidence linking the use of the test to health outcomes is not available, the panels should answer the following questions, which collectively determine whether there is convincing indirect evidence that the test will lead to better health outcomes:
Question 1: Is the evidence adequate to determine that the use of the test provides more accurate diagnostic information?
The definition of "more accurate" is crucial. The standard measures of accuracy are sensitivity (probability of a positive test result in a patient with a disease or risk factor or other health condition) and specificity (the probability of a negative test result in a patient who does not have the disease). Ideally a new test would increase both sensitivity and specificity. Often that is not the case. A test that has a higher sensitivity is not unambiguously more accurate than an alternative test unless its specificity is at least as great. For most diagnostic tests, a change in the definition of an abnormal result will change the sensitivity, but improved sensitivity is obtained at the cost of worsened specificity, and vice versa. For example, if the diagnosis of diabetes is made on the basis of a fasting blood sugar, the use of a lower blood sugar level to define diabetes results in greater sensitivity and lowered specificity when compared to a diagnostic threshold at a higher blood glucose level. By choosing a different threshold, it is possible to change sensitivity without changing the test. Thus, if only sensitivity (or specificity) were considered, the same test might appear more accurate solely because the definition of an abnormal test result was changed.
The foregoing discussion leads to the following definition of "more accurate:" A more accurate test is not only more sensitive (or specific); it has a higher sensitivity for a given level of specificity when compared to another test. At a minimum, then, to conclude that one test is more accurate than another, its sensitivity (or specificity) is must be higher while its specificity (or sensitivity) is the same or better than the alternative test or diagnostic strategy.1
In deciding whether one test is more accurate than a second, established test, the panels will find the following steps helpful.
Step 1: Evaluate the quality of studies of test performance
The panel should first address the quality of the studies that are used to determine test accuracy. In assessing the quality of studies, panels might first consider the characteristics of an "ideal" study of test accuracy and compare the existing studies to the ideal. "Ideal" and "typical" studies of a screening, diagnostic, or monitoring test differ in these ways:
| Ideal study |
Usual study |
Effect of Usual Study |
| The study subjects are consecutive patients seen in a typical clinical setting with a chief complaint. |
Subjects selected because they had the diagnostic gold standard. |
Overestimates sensitivity and underestimates specificity |
| All patients who get the index test also get the reference test |
Patients with negative results on the index test often don’t get the diagnostic gold standard |
Overestimates sensitivity and underestimates specificity |
| The person who interprets the index test is blinded to all other information |
The person who interprets the index knows the clinical history and the results of the diagnostic gold standard. |
Overestimates sensitivity and specificity. |
| The person who interprets the reference test is blinded to all other information |
The person who interprets the diagnostic gold standard knows the clinical history and the results of the index test. |
Overestimates sensitivity and specificity. |
| The reference test is a valid measure of the disease state |
The diagnostic gold standard imperfectly measures the disease state. |
The measured test performance could either be worse or better than the true performance. |
*The reference test is a test that is considered the "gold standard," i.e., a test that is used to define the disease. Tests commonly used as reference tests are coronary angiography, for coronary artery disease, and histopathology, for cancer. Reference test can be interpreted more broadly to mean any method that is considered the definite basis for determining whether a disease or risk factor is truly present.
The panels will need to decide whether the results of studies that fall short of the ideal are likely to be due to bias, or whether their limitations are sufficiently minor that it is possible to draw conclusions about the accuracy of the test.
Step 2: Evaluate the possibility that the two tests are complementary
The sensitivity and specificity of a new test can be the same as - or even worse than - the sensitivity and specificity of an established comparison test, yet still provide valuable information. It can add value if it provides complementary information. In this circumstance, a combination of the two tests leads to more accurate distinction between patients with and without the disease (or risk factor) than either test individually. The information is likely to be complementary if the other test or tests detect other features of the disease (for example, one test measures a physiological phenomenon while the other is an imaging test that detects structural abnormalities). A direct comparison between strategies using the two tests and those using only the standard test can be made by studying patients who receive both tests as well as the reference test (or any direct measure of whether disease is actually present). The appendix describes how such a study can be used to determine whether the combined testing strategy improves the accuracy of diagnosis.
Question 2: If the test improves accuracy, is the evidence adequate to conclude that the improved accuracy will lead to better health outcomes?
To determine whether a difference in test accuracy would lead to important improvements in health outcomes, the panels may find the following steps helpful.
Step 1: Calculate the post-test probability of disease
The purpose of testing is to reduce uncertainty about the presence of a disease or risk factor, or about the extent of a previously diagnosed disease. The pre-test probability of disease is the probability of disease before the test has been performed, based upon history, physical examination, and preliminary diagnostic tests. The pre-test probability is often used interchangeably with the term "disease prevalence," but the two terms are only equivalent when prevalence and pre-test probability are based on the same population (i.e, adjusted for history and other information).
The post-test probability is the probability of disease after learning the test results. A test result should only change patient management if it changes the probability of disease. Bayes' theorem is the formal approach used to calculate the post-test probability. Application of Bayes' theorem in this context requires the sensitivity and specificity of the test and the pre-test probability of disease. Generally, tests alter probability the most (i.e., in comparison to the pre-test probability) when the pre-test probability is intermediate (i.e., not near a probability of either 0 or 1). Conversely, tests alter probability the least when the pre-test probability is close to zero or close to 1.0. If the patient's symptoms, abnormalities on physical examination, and other evidence strongly suggest that the patient has the disease in question (i.e., the pre-test probability of disease is high), unless a test is extremely sensitive the patient is likely to have the disease even if the test result is negative, and should be managed accordingly. Similarly, if the pre-test risk of disease is very low, the probability of disease in a patient with a positive test result remains very low, unless the test is extremely specific (i.e., rarely produces false-positive results). The accompanying graph of post-test probability for two tests illustrates this point. Panels may find these graphs helpful in interpreting the possible impact of a difference in test performance.
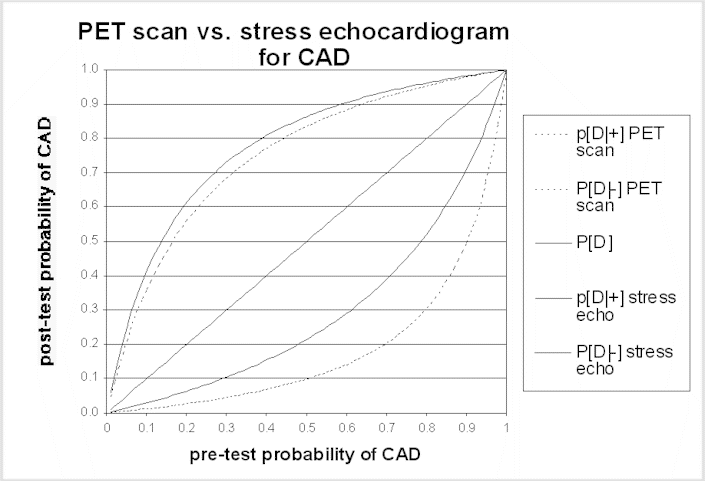
The same principles apply to the use of testing to stage disease or to monitor the effect of treatment. In these situations, the uncertainty is not about the diagnosis, but the test is needed to reduce uncertainty about the current status of the disease. Learning more about stage or response to treatment is important insofar as it will influence management options - for example, disease progression while on one treatment will often lead to a change in therapies, or cessation of a potentially toxic therapy. A false-negative staging test result (i.e., one that implies the disease is more limited than it really is) may lead to treatment that is both ineffective and harmful. In some situations, a false-positive staging test result can have even more harmful consequences; the physician could withhold potentially curative treatment if he or she interprets the staging test as indicating that cure is not possible, dooming a patient to die of a disease that could have been treated effectively.
Step 2: Evaluate the potential impact on management when tests differ in the post-test probability:
In the absence of direct evidence of the effects of a test on health outcomes, it will sometimes be possible to conclude with great confidence that improved accuracy will lead to better outcomes. This is particularly likely to be true when the treatment or management strategy is effective for patients with the disease, but poses risks or discomfort that would not be acceptable when administered to patients who do not have the disease. Then, improved accuracy leads to effective treatment for more people who truly have the disease, and helps avoid unnecessary treatment in people who would not benefit from it. Thus, although the evidence that diagnostic tests for cancer and for heart disease alter health outcomes is largely indirect, it is also compelling. For these categories of disease, there is often strong evidence that treatments with significant adverse consequences are effective when used appropriately. Panels will need to judge whether the test leads to better patient management by increasing the rate at which patients with disease receive appropriate treatment and the rate at which patients who do not have the disease avoid unnecessary treatment.
If management changes, the improvement in health outcomes should be large enough that the panel believes it is clinically significant. A small increase in accuracy can lead to substantial improvements in health outcomes if treatment is highly effective. Improved accuracy is of little consequence, however, if treatment is either ineffective, so there is little benefit to patients with the disease, or very safe, so there is little harm to patients without the disease. Then improved accuracy is unlikely to lead to improved health outcomes or even to influence clinical decisions.
Under exceptional circumstances, prognostic information, even if it did not affect a treatment decision, could be considered to improve health outcomes. The panel should be alert for circumstances in which patients would be likely to value the prognostic information enough to significantly alter their well-being.
Summary
The recommended approach for evaluating diagnostic tests is as follows:
- Review, when available, high quality studies that provide direct evidence that test results improve health outcomes.
- If there is no high quality direct evidence, evaluate the indirect evidence as follows:
Decide whether studies of test accuracy are sufficiently free of bias to permit conclusions about the accuracy of the test under consideration, in comparison either to another test or another screening, diagnostic, or staging strategy
Evaluate the potential impact of improved accuracy (or complementary information) on health outcomes. Evaluating the effect of test accuracy on post-test probability is one part of this step. The other part is deciding whether the change in patient management that results from the test will improve health outcomes. Improved outcomes are likely to occur when the management strategy is effective in patients with the disease and does not benefit those without the disease. A test can also improve health outcomes when the treatment poses significant risk, so that it is very important to avoid unnecessary treatment.
APPENDIX: THE ADDED VALUE OF COMBINED TESTING
To test the hypothesis that two tests are complementary, several approaches are possible. The best way is a study in which a series of patients receive both tests as well as the reference test. The analysis compares the sensitivity of the second test in two groups of patients: those with a negative result on the first test and those with a positive result, as shown in the table.
| |
Test 1 results positive |
Test 1 results negative |
Test 2 results |
Reference standard positive |
Reference standard negative |
Reference standard positive |
Reference standard negative |
Positive |
A |
|
A’ |
|
Negative |
B |
|
B' |
|
Totals |
A+B |
|
A'+B' |
|
If the sensitivity of Test 2 when test 1 is negative (A'/[A'+B']) is greater than zero, Test 2 is able to detect patients that Test 1 cannot, and the two tests are complementary. If, on the other hand, the sensitivity of Test 2 is zero when Test 1 is negative, Test 2 is unable to detect patients that Test 1 would miss, and it is of minimal additional value.
Many studies of two tests do not provide the information in this table. However, the studies may still provide useful data that reflect what is in the table. The best way to think about using two tests is to consider them as a sequence of tests, in which the post-test probability after the first test becomes the pre-test probability for the second test. Suppose that the test under consideration is the second test in the sequence. It would add information when compared to the established test alone under two circumstances:
- The first test in the sequence is positive, and the post-test probability after a positive result on the second test in the sequence is greater than the post-test probability after the first test.
- The first test in the sequence is negative, and the post-test probability after a negative result on the second test in the sequence is lower than the post-test probability after the first test.
Arguments that consist largely of inductive reasoning (based upon a different physiological basis for Test 2) are much weaker than empirical eevidence.
1 The more technical expression of this condition is that a more accurate test is one whose receiver operating characteristic (ROC) curve is above and to the left of the ROC curve for the alternative test.


